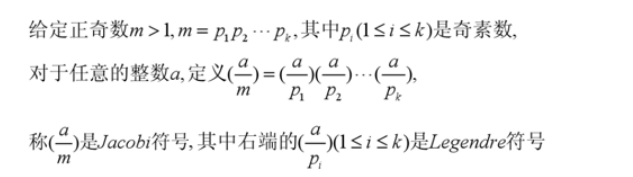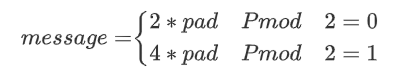DASCTF-CBCTF-crypto部分赛题复现

2023-10-29

未分类

2.5k 词

好忙TvT，做密码和学web两难全啊。

EzRSA

源码：

from Crypto.Util.number import *
import random
from gmpy2 import *
from libnum import *
from flag import flag

def padding(f):
    random_chars = bytes([random.randint(0, 255) for _ in range(32)])
    f = f + random_chars
    return f

def guess_p(p):
    e = 65537
    
    P = p
    n1 = getPrime(512)*getPrime(512)
    with open('enc.txt', 'w+') as f:
        while jacobi(2,n1) == 1:
            n1 = getPrime(512)*getPrime(512)
        while P:
            pad = random.randint(0, 2**2023)**2 
            message = pad << 1 + P % 2
            cipher = pow(message, e, n1)
            f.write(str(cipher)+'n')
            P //= 2
    print("n1 = "+ str(n1) )    
    
def guess_q(q):
    
    def encrypt(q, n):
        e = random.randint(1000,2000)
        noise = random.randint(0, n - 1)
        c = pow(q+noise,e,n)
        return e, noise,c 
    
    n2 = getPrime(512)*getPrime(512)
    e1, noise1, c1 = encrypt(q, n2)
    e2, noise2, c2 = encrypt(q, n2)
    print("n2 = "+ str(n2) ) 
    print('(e1, noise1, c1) =', (e1,noise1,c1))
    print('(e2, noise2, c2) =', (e2,noise2,c2))

p = getPrime(512)
q = getPrime(512)

n = p*q
guess_p(p)
guess_q(q)
e = 0x10001
flag = padding(flag)
m = bytes_to_long(flag)
c = pow(m,e,n)

print("c = " + str(c))
'''
n1 = 65634094430927080732256164808833233563732628654160389042977689628512527168256899310662239009610512772020503283842588142453533499954947692968978190310627721338357432052800695091789711809256924541784954080619073213358228083200846540676931341013554634493581962527475555869292091755676130810562421465063412235309
n2 = 103670293685965841863872863719573676572683187403862749665555450164387906552249974071743238931253290278574192713467491802940810851806104430306195931179902098180199167945649526235613636163362672777298968943319216325949503045377100235181706964846408396946496139224344270391027205106691880999410424150216806861393
(e1, noise1, c1) = (1743, 44560588075773853612820227436439937514195680734214431948441190347878274184937952381785302837541202705212687700521129385632776241537669208088777729355349833215443048466316517110778502508209433792603420158786772339233397583637570006255153020675167597396958251208681121668808253767520416175569161674463861719776, 65643009354198075182587766550521107063140340983433852821580802983736094225036497335607400197479623208915379722646955329855681601551282788854644359967909570360251550766970054185510197999091645907461580987639650262519866292285164258262387411847857812391136042309550813795587776534035784065962779853621152905983)
(e2, noise2, c2) = (1325, 35282006599813744140721262875292395887558561517759721467291789696459426702600397172655624765281531167221787036009507833425145071265739486735993631460189629709591456017092661028839951392247601628468621576100035700437892164435424035004463142959219067199451575338270613300215815894328788753564798153516122567683, 50327632090778183759544755226710110702046850880299488259739672542025916422119065179822210884622225945376465802069464782311211031263046593145733701591371950349735709553105217501410716570601397725812709771348772095131473415552527749452347866778401205442409443726952960806789526845194216490544108773715759733714)
c = 124349762993424531697403299350944207725577290992189948388824124986066269514204313888980321088629462472088631052329128042837153718129149149661961926557818023704330462282009415874674794190206220980118413541269327644472633791532767765585035518183177197863522573410860341245613331398610013697803459403446614221369
'''

题解：

第一部分 Guess p

这部分不是我出的，是队友找到了类似的题目

https://blank-vax.github.io/2019/10/30/%E4%B8%A4%E9%81%93CTF-RSA%E7%B1%BB%E9%A2%98%E7%9B%AE%E6%80%BB%E7%BB%93/

队友改的脚本：

import gmpy2

path = "enc.txt"

N = 65634094430927080732256164808833233563732628654160389042977689628512527168256899310662239009610512772020503283842588142453533499954947692968978190310627721338357432052800695091789711809256924541784954080619073213358228083200846540676931341013554634493581962527475555869292091755676130810562421465063412235309
e = 0x10001
two_inv = pow(gmpy2.invert(2, N), e, N)

with open(path, 'r') as f:
    p = ''
    data = f.read().split("n")[:-1]
    for ct in data:
        ct = int(ct)
        jacobi = gmpy2.jacobi(two_inv * ct, N)
        if jacobi == -1:
            p = '1' + p 
        else:
            p = '0' + p

print(int(p,2))

原理分析：

关于雅克比符号：雅克比符号是勒让德符号的推广。

勒让德符号定义如下：

二次剩余指有解，则a是模p的二次剩余

雅克比符号定义如下：

二次互反律：

接下来对题目具体分析：

随机数

message = pad << 1 + P % 2

考虑到优先级，这里应该是message = pad << (1 + P % 2)

所以：

推得

为二次剩余形式。

表示的低位,表示按顺序输出的,

根据上述雅克比符号与勒让德符号相关定义，当时，则有解

计算

//e为奇数，去掉后结果不变

//，因为对于显然有解，则雅克比符号为1

显然时，有解，雅克比符号为1;因为有,根据二次互反律，时,雅克比符号为-1

根据这个，不和博文里一样乘2的逆元应该是用相反的方式取值，但是最后没有跑出来一样的结果，有点奇怪。

对于正确解的推导同上，雅克比符号为-1时取1，反之取0

第二部分 Guess q

之前七月赛复现过这个内容2023DSACTF——Crypto题目复现 | crumbling’s secret room (fcrumbling.github.io)，相关明文攻击，这里用的是另一个方法Gr¨obner bases，也是当时就发现的可替代方案。

from Crypto.Util.number import *
n2 = 103670293685965841863872863719573676572683187403862749665555450164387906552249974071743238931253290278574192713467491802940810851806104430306195931179902098180199167945649526235613636163362672777298968943319216325949503045377100235181706964846408396946496139224344270391027205106691880999410424150216806861393
(e1, noise1, c1) = (1743, 44560588075773853612820227436439937514195680734214431948441190347878274184937952381785302837541202705212687700521129385632776241537669208088777729355349833215443048466316517110778502508209433792603420158786772339233397583637570006255153020675167597396958251208681121668808253767520416175569161674463861719776, 65643009354198075182587766550521107063140340983433852821580802983736094225036497335607400197479623208915379722646955329855681601551282788854644359967909570360251550766970054185510197999091645907461580987639650262519866292285164258262387411847857812391136042309550813795587776534035784065962779853621152905983)
(e2, noise2, c2) = (1325, 35282006599813744140721262875292395887558561517759721467291789696459426702600397172655624765281531167221787036009507833425145071265739486735993631460189629709591456017092661028839951392247601628468621576100035700437892164435424035004463142959219067199451575338270613300215815894328788753564798153516122567683, 50327632090778183759544755226710110702046850880299488259739672542025916422119065179822210884622225945376465802069464782311211031263046593145733701591371950349735709553105217501410716570601397725812709771348772095131473415552527749452347866778401205442409443726952960806789526845194216490544108773715759733714)
P.<q,m0>=PolynomialRing(Zmod(n2))
f1=(q+noise1)^e1-c1
f2=(q+noise2)^e2-c2
F=[f1,f2]
B=Ideal(F).groebner_basis()
print(B)
#[q + 103670293685965841863872863719573676572683187403862749665555450164387906552249974071743238931253290278574192713467491802940810851806104430306195931179902084990861262304328268863425199809518254496553684067856859306280794877830073274539837451563189724268783548897996668966918676147376205691514341926655798880936]
q=(-B[0])%n2
print(q)
#-q + 13189337905641321257372188436353844418280745284875462357019668708167547026960641869513283218672677712590326347601424108528959315675307896082223561007980457

第三部分常规的求解m：

from Crypto.Util.number import *
from gmpy2 import *
p=9473204278465588641589315677772678997836862033858760337441231265335880892205102590571357305720744128962068300763212493598006400853597404586755248901932203
q=13189337905641321257372188436353844418280745284875462357019668708167547026960641869513283218672677712590326347601424108528959315675307896082223561007980457
c=124349762993424531697403299350944207725577290992189948388824124986066269514204313888980321088629462472088631052329128042837153718129149149661961926557818023704330462282009415874674794190206220980118413541269327644472633791532767765585035518183177197863522573410860341245613331398610013697803459403446614221369
phi=(p-1)*(q-1)
e = 0x10001
d=gmpy2.invert(e,phi)
m=pow(c,d,p*q)
print(long_to_bytes(m))

CB backpack

源码：

from random import shuffle

def gen_e():
    e = []
    for i in range(8):
        ee = [0]*3+[1]*3
        shuffle(ee)
        e += ee
    return e
    
e = gen_e()
nbit = len(e)
flag = 'DASCTF{'+sha256(''.join([str(i) for i in e]).encode()).hexdigest()+'}'

a = [randint(1,2^nbit) for i in range(nbit)]

re = 0
for i in range(nbit):
    re += e[i]*a[i]

print(a)
print(re)
#[65651991706497, 247831871690373, 120247087605020, 236854536567393, 38795708921144, 256334857906663, 120089773523233, 165349388120302, 123968326805899, 79638234559694, 259559389823590, 256776519514651, 107733244474073, 216508566448440, 39327578905012, 118682486932022, 263357223061004, 132872609024098, 44605761726563, 24908360451602, 237906955893793, 204469770496199, 7055254513808, 221802659519968, 169686619990988, 23128789035141, 208847144870760, 272339624469135, 269511404473473, 112830627321371, 73203551744776, 42843503010671, 118193938825623, 49625220390324, 230439888723036, 241486656550572, 107149406378865, 233503862264755, 269502011971514, 181805192674559, 152612003195556, 184127512098087, 165959151027513, 188723045133473, 241615906682300, 216101484550038, 81190147709444, 124498742419309]
#4051501228761632

非预期：

因为背包（构成的格）的密度过大，直接用原数据进行LLL算法无法求解

背包的密度

$（）$

指物品权值的最大值，即最大值；n指物品个数，即的个数

预期解：

本题原型是构造一个RSSP问题，但是为了方便filter就给了更加强大的约束，即背包的八块都是balanced的情况，预期是实现一个HJ算法（New generic algorithms for hard knapsacks）或者BCJ算法（Improved Generic Algorithms for Hard Knapsacks)），去进行求解。

RSSP（Randomized Subset Sum Problem）集合的子集求和问题的一个变种。

假设有一个有限的整数集合，以及一个整数 b。 SSP 问题的目标是找到一个整数子集 T，其中 T ⊆ S，使得子集 T 的元素之和 ΣT 等于整数 b。

SSP 问题的变种之一是 Randomized SSP，即RSSP。在 RSSP 中，对于每个元素，我们引入一个随机比特，取值为0或1。问题变成了在给定元素和目标整数 b 的情况下，找到一个子集 T，使得。

The algorithm of Schroeppel and Shamir

The Howgrave-Graham–Joux Algorithm

写到一半被告知exp用的是The algorithm of Schroeppel and Shamir，泪目了T T.

exp没跑动，暂且搁置了

论文New generic algorithms for hard knapsacksHJ算法的第三节讲的就是这个算法，就照着上面的看了，一二节的基础部分内容也就不删除了。

【警告：gpt翻译+菜鸡解读】

一些符号的含义：

背包：

背包的个数：n

目标：S

系数:（0或1）

权重:

背包的密度：d

1.Introduce部分摘要：

d<0.94该问题可以用LLL算法解决，d>1时有基于格规约的变体攻击可以成功碰撞，但对于接近1，也就是(0.94,1)区间，没有比较好的格规约的攻击方式，本文则是提出相关算法。

2.Background on knapsacks部分摘要：

几个种类的背包的介绍，这里暂不展开,在需要的时候再添加（有点忙，小偷个懒）

Modular knapsacks

2.2Random knapsacks

2.3Unbalanced knapsacks

不平衡的背包

随机背包权重,然而，大多数时候，我们预计其权重将接近n/2。由于各种原因，考虑带有不同重量的背包也很有用。我们定义一个具有 n 个元素的 α-不平衡随机背包，根据给定的 α 和密度 d，如下所示：

令
在 $，$ 中均匀随机选择每个（对于i从1到n）
这一点没看懂，等我之后再来补
令$l=⌊αn⌋$并均匀地选择一个随机向量r,在 $\begin{pmatrix} n\\ l \end{pmatrix}$ 这样的向量集合中的坐标正好等于1,其余的都是0，令$S=Σ_{i=1}^n(a_i r_i)$ [没看懂]

不平衡的背包是很自然需要考虑的，因为它们已经出现在基于格的算法中，其中 α 的值会极大地影响可以攻击的密度。此外，在我们的算法中，即使在最初解决普通背包问题时，不平衡的背包也可能在计算过程中出现。

当处理正好一半是 0 和一半是 1 的平衡背包时，我们也使用上述的定义，并称其为 1/2-不平衡的背包。

2.4Complementary knapsacks

互补背包

给定一个背包和目标S，我们将它的互补背包定义为包含相同元素并具有目标的背包，具体性质原背包与互补背包满足关系

因此，解决这两个背包中的任何一个也会得到另一个背包的结果。并且权重与满足。

特别是，如果一个背包是α-不平衡的，它的互补背包是（1−α）-不平衡的。因此，在任何算法中，我们都可以不失一般性地假设或

Asymptotic values of binomials

Distribution of random knapsack sums

提到了1个定理和4个推论：

内容大致为：

3.The algorithm of Schroeppel and Shamir：

本节应该是讲述了介绍部分提到的Schroeppel-Shamir 算法的一些相关内容,因为HJ算法是对该算法的优化。

来自Lazzaro佬：
Schroeppel-Shamir Algorithm
时间复杂度,空间复杂度均为 O(n/2)
The Howgrave-Graham–Joux Algorithm
时间复杂度 O(0.337n)，空间复杂度 O(0.256n)
BCJ算法则是针对高密度背包问题下1的数量已知的特解方法

画外音：L的大哥说HJ和BCJ都是都SS算法的优化，而且是仅针对于背包问题的。

Schroeppel和Shamir算法是一种用于解决n元素的通用整数背包问题的算法。该算法改进了生日悖论/生日攻击，能够找到背包问题的所有解。

3.1 Schroeppel 和 Shamir 算法的变种

3.2 Application to unbalanced knapsacks

针对unbalanced knapsacks的应用

4 The new algorithms

The Howgrave-Graham–Joux Algorithm的提出

4.1基本原理

在本节中，我们想解决一个关于n个元素的通用背包问题。我们从基本的背包方程式开始：

如第2节所述，如果需要，通过使用Complementary knapsacks，我们可以假设

参考资料

DASCTF-CBCTF 2023 - ZimaB1ue - 博客园 (cnblogs.com)

两道CTF-RSA类题目总结 | B1ank (blank-vax.github.io)

分析N1CTF 2019中Crypto方向题目-安全客 - 安全资讯平台 (anquanke.com)

⁢⁤‌‬‬⁢⁣‍⁡⁡⁣⁣⁤‌⁢‬⁣⁡⁤‌⁣⁡⁡⁡⁣‬⁡DASCTF x CBCTF - 飞书云文档 (feishu.cn)

New generic algorithms for hard knapsacks

https://eprint.iacr.org/2011/474.pdf

其他加密算法 | Lazzaro (lazzzaro.github.io)

密码学系列之:生日攻击 - 知乎 (zhihu.com)https://zhuanlan.zhihu.com/p/379077249)

标签

归档

最新文章

DASCTF-CBCTF-crypto部分赛题复现

EzRSA

第一部分 Guess p

第二部分 Guess q

第三部分常规的求解m：

CB backpack

The algorithm of Schroeppel and Shamir

1.Introduce部分摘要：

2.Background on knapsacks部分摘要：

3.The algorithm of Schroeppel and Shamir：

4 The new algorithms

参考资料

标签

归档

最新文章

EzRSA

第一部分 Guess p

第二部分 Guess q

第三部分 常规的求解m：

CB backpack

The algorithm of Schroeppel and Shamir

1.Introduce部分摘要：

2.Background on knapsacks部分摘要：

3.The algorithm of Schroeppel and Shamir：

4 The new algorithms

参考资料

第三部分常规的求解m：